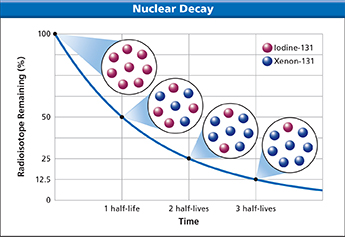
Figure 9 The half-life for the beta decay of iodine-131 is 8.07 days. After one half-life (8.07 days), half of a sample of iodine-131 will have decayed into xenon-131. After two half-lives (16.14 days), three quarters of the sample will have decayed.
 d
dHalf-Life
A nuclear decay rate describes how fast nuclear changes take place in a radioactive substance. Every radioisotope decays at a specific rate that can be expressed as a half-life. A half-life is the time required for one half of a sample of a radioisotope to decay. After one half-life, half of the atoms in a radioactive sample have decayed, while the other half remain unchanged. After two half-lives, half of the remaining half decays, leaving one quarter of the original sample unchanged. Figure 9 illustrates the nuclear decay rate of iodine-131. Iodine-131 has a half-life of 8.07 days. After two half-lives, or 16.14 days, the fraction of iodine-131 remaining is one quarter. After three half-lives, or 24.21 days, the fraction of iodine-131 remaining is one half of one quarter, or one eighth.
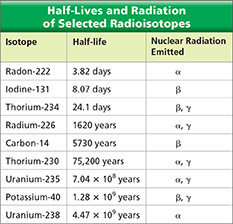
Half-lives can vary from fractions of a second to billions of years. Figure 10 lists the half-lives of some common radioisotopes. Uranium-238, for instance, has a half-life of 4.5 billion years. This means that in 4.5 billion years, there will be half as much uranium-238 on Earth as there is today. You could also say that 4.5 billion years ago, there was twice as much uranium-238 on Earth as there is today.  Unlike chemical reaction rates, which vary with the conditions of a reaction, nuclear decay rates are constant. Regardless of the temperature, pressure, or surface area of a uranium-238 sample, its half-life is still 4.5 billion years.
Unlike chemical reaction rates, which vary with the conditions of a reaction, nuclear decay rates are constant. Regardless of the temperature, pressure, or surface area of a uranium-238 sample, its half-life is still 4.5 billion years.
Figure 10 Nuclear decay rates are constant. A given radioisotope decays at a specific rate, or half-life. Calculating What isotope is produced by the nuclear decay of radon-222?
 dd
dd
What is a half-life?




